Early in life, humans first learn to walk, and then a few years later, they learn to ride bicycles, and finally, as young adults, they learn to drive cars. In learning how to do each new task, humans don’t forget previous ones. Artificial neural networks, on the other hand, struggle to learn continually and consequently suffer from catastrophic forgetting: the tendency to lose almost all information about a previously learned task when attempting to learn a new one.
In this post, I will describe the technicalities of why neural networks do not learn continually, briefly discuss how the brain is thought to succeed at learning task after task, and finally highlight some exciting work in the machine learning community that builds on fundamental principles of neural computation to alleviate catastrophic forgetting.
Catastrophic forgetting in neural networks
Why do neural networks forget previously learned tasks so easily after learning a new one? Each task that a neural network learns to perform has a single error function that the network is trying to minimize, irrespective of the error of any other task. To be more specific, a typical neural network has a set of weights and biases, which are its parameters. For the network to change its behavior or learn how to perform a task, it must change its parameters, and this is exactly what happens during training. The figure below shows the weight space of a neural network: each axis corresponds to the value of a single parameter (imagine there are only two parameters for illustration purposes, but in reality there could be millions of dimensions). At any point in time, a typical neural network is at a single place in weight space based on its parameters’ values. Then, learning is equivalent to moving throughout weight space to a place where the error is small on the task being learned.
Say we have two tasks to be learned in sequence: distinguishing between different species of birds, and identifying various handwritten Greek letters. As a randomly initialized neural network learns to classify different species of birds, it will move through weight space to a place where the error on this task is low. Then, it will attempt to learn Greek letters. Just as before, it will move to a place where the error will be low on this new task. The places in weight space where the network can reliably identify different handwritten Greek letters are likely to be separate from those where it previously achieved success classifying bird types, especially since weight space is typically millions of dimensions.
In the diagram below, the orange circle represents the neural network at a place in weight space, and the areas shaded in green and purple correspond to where the error on learning a wide array of birds and greek letters is sufficiently small, respectively.
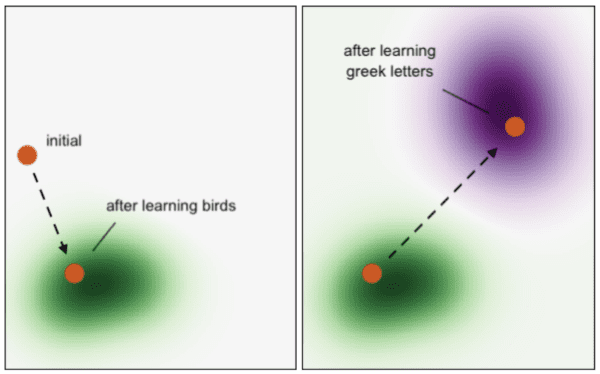
So what just happened? When the network tried to learn handwritten Greek letters, it completely ignored what places in weight space are relevant to the previous task it learned, and hence it forgot how to distinguish between different species of birds. As a side note, the two areas where the neural network performs well on each task may overlap, but this is typically not the case due to the high number of dimensions in weight space. Additionally, even if the two areas coincide, when the neural network learns the latter task in isolation, it may find a place that’s only good for the second task.
Some theories about how brains continually learn
Neuroscientists have long been aware about the existence of pyramidal neurons in the cortex, and these neurons are quite different from the artificial neurons used by contemporary neural networks. Each pyramidal neuron has hundreds of dendrites, which receive signals along incoming synapses from other neurons. The role of each dendrite is to detect a different input pattern to the neuron, and if a certain pattern is detected, the neuron will be depolarized, i.e., more likely to become active. Only a fraction of the input signals received by a neuron along incoming synapses are able to make that neuron active, and dendrites essentially determine which signals affect the neuron.
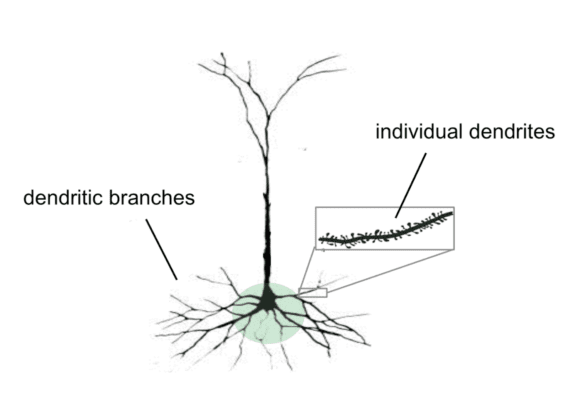
Moreover, the patterns detected by dendrites are highly sparse (as neural activations are sparse in general) and less likely to interfere with each other. According to the Thousand Brains Theory of Intelligence, this likely explains why humans are able to learn continually without catastrophic forgetting. When a person has a novel experience, dendrites ensure that only a subset of incoming synapses are modified for learning purposes (precisely those that yielded the sparse activity pattern). Other synaptic connections established as a result of previous experiences remain largely untouched, and thus are not overwritten. This is unlike in neural networks, where all parameters are updated via backpropagation of errors.
Towards artificial brain-like continual learning
Over the past few years, researchers have taken inspiration from the brain to address continual learning in neural networks. Elastic Weight Consolidation and Intelligent Synapses, two methods that have received considerable attention, constrain how freely each parameter can move throughout weight space when learning a new task so that those which are deemed important towards performing previous tasks are not altered much. This is similar in spirit to how many incoming synapses to a pyramidal neuron don’t get modified through novel experiences. However, one clear downside to this approach is that it doesn’t scale well to longer sequences of tasks, as parameters in a neural network become more constrained with each new task learned, making tasks later in the sequence harder to learn.
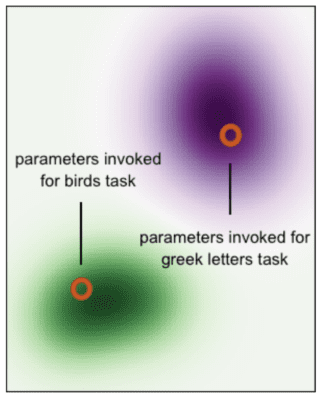
In contrast to parameter-constraining methods, we can instead construct models that use just a subset of their parameters to perform each task, just as the brain only employs a subset of synapses to transmit signals via the use of dendrites. In the context of our diagram of error objectives above, this idea corresponds to a single model becoming active at multiple places in weight space based on which subset of parameters it invokes (technically, the model still occupies just one place in weight space, but by invoking different subsets of parameters, it essentially operates in distinct subspaces, and can do so in a way that is beneficial to all tasks). Now, when a continual learner wants to learn various tasks in sequence, different subsets of parameters are invoked for each distinct task, just how the signals received along different incoming synapses become more relevant for neurons in the cortex. In theory, this solves catastrophic forgetting.
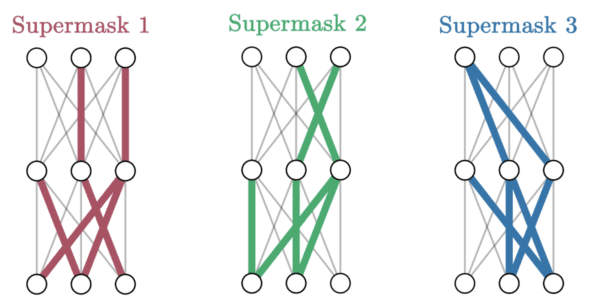
The exciting news is that this new approach has already started to appear in the machine learning community. The idea behind Supermasks is to select a subset of artificial neurons in a standard neural network to learn and perform each unique task. This works quite well in some tasks, and scales to an exponential number of tasks in the number of artificial neurons in the network, a huge computational improvement over Elastic Weight Consolidation.
Another related idea is a Gated Linear Network, which is a neural network where each artificial neuron has multiple parameters and selects which one to apply to the input based on information about the task. As mentioned, neurons in the brain are much more sophisticated than those in regular neural networks, and the artificial neurons used by Gated Linear Networks capture more detail and somewhat replicate the role of dendrites. They also show improved resilience to catastrophic forgetting.
The brain is highly sparse, and researchers have invested enormous efforts modeling its sparsity and enabling efficient computation in neural networks. In this post, we explored why continual learning in neural networks generally fails, and how the theme of sparsity plays an integral role in overcoming catastrophic forgetting in both biological and artificial systems. The path to continual learning without catastrophic forgetting will likely rely on some sort of sparsity, which is already well documented both in biology and computational modeling. For a more granular overview of continual learning, see the review paper below.

